CSC212 Lab 12 2014

--D. Thiebaut (talk) 19:37, 9 November 2014 (EST)

---

This lab deals with Sorting algorithms, HeapSort, QuickSort, and methods used to avoid worst-case conditions.

Lab Problem #0: Observing Quicksort at Work

• Point your Firefox or Safari browser to this URL: http://cs.smith.edu/~thiebaut/java/sort/. Chrome won't work with 64-bit Java Applets, so no need to try it...
• You may need to resize the window or shrink/expand the applet to see the Start Button.

Standard Quicksort, Random Array

• Select Standard Quicksort for the Sorting Algorithm
• Select Random for the Array Type
• Select Swap Square for the View
• Delay of 25
• Start!
• Notice how partition works. Whatever group of bars is red represent the partition that is being split into 2 around the pivot.
• Don't hesitate to run the experiment a few times until you "get it".

Standard Quicksort, Array in Increasing Order

• Click Stop so that you can start a new experiment.
• Select Standard Quicksort for the Sorting Algorithm
• Select Sorted Incr. Order for the Array Type
• Select Swap Square for the View
• Delay of 25
• Start!
• Notice how the partition is of size N first, then N-1, then N-2, etc.

Standard Quicksort, Array in Decreasing Order

• Click Stop so that you can start a new experiment.
• Select Standard Quicksort for the Sorting Algorithm
• Select Sorted Decr. Order for the Array Type
• Select Swap Square for the View
• Delay of 25
• Start!
• Notice how the partition is of size N first, then N-2, then N-4, etc.

Quicksort with a Random Pivot

• Repeat the same experiments above, (random array, sorted in increasing order, sorted in decreasing order), but pick "Quicksort with Random Pivot" as the algorithm.
• Does the random pivot help with the random array?

Quicksort with Tail Recursion Truncated

• Same experiments again, but this time pick the "Quicksort with Tail Recursion Truncated" algorithm. Try to answer the following questions to yourself, as a way of understanding how tail recursion works for Quicksort. Nothing to submit anywhere...

Question 1

Can you see the tail recursion being truncated? Which sorting method is used to sort the small partitions?

Question 2

Is the O(N^2) sorting routine called on all the small partitions, separately, or is it called on the whole array?

Question 3

Can you explain the two areas identified below?

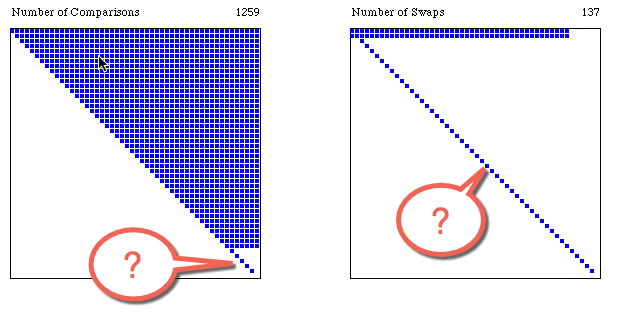
Question 4

Is the Quicksort algorithm cutting the tail recursion, also using a random pivot or not?

Lab Problem #1: Recursion-Stack Depth

• Create a class containing the code for Quicksort.
• Run it on arrays of size 10, 200, 500, 1000, 5000, 10000, 50000, 100000. Keep on increasing the size until something happens...
• You probably ran into an exception... Make sure you read what the exception is... Can you figure it out?
• Read the documentation of the -XSS command line on this page.
• Apply it to your program

• If you are using Eclipse, click on the Run top menu-option, then Run Configurations, then on the Arguments tab, and in the VM arguments window, enter something like -Xss4m (you'll have to do go through some trials and errors to find the right value.
• If you are running your Java code on beowulf, simply add the option on the command line for the Java Virtual Machine (in this case, a request for 64 Megabytes of stack size):

java -Xss64m QuickSort 1000000 random

• Make sure you have define a large enough stack to sort at least a million ints.

Lab Problem #2: HeapSort

• Java provides heap data structures, but calls them PriorityQueues.
• Instead of keeping the largest element at the top of the heap, PriorityQueues keep the smallest element at the top.
• Try the example below to see how to use a PriorityQueue

        import java.util.PriorityQueue;
	
	public static void TestPrioQueues() {

		PriorityQueue<Integer> heap = new PriorityQueue<Integer>();

		heap.add( 1 );
		heap.add( 20 );
		heap.add( 5 );
		heap.add( 100 );
		while ( ! heap.isEmpty() )
			System.out.println( heap.poll() );
	}

Question 1

Using some of the code/functions from this page, create a function called heapsort( int[] A ) that will use a priority queue to sort the array of ints A.

Question 2

Using the code snippet below, measure the execution times of QuickSort and of your HeapSort function. Figure out which is regularly faster on arrays of varying sizes.

        long start = System.nanoTime();
        quicksort(A, 0, A.length - 1);
        long end   = System.nanoTime();
        System.out.println( String.format(   
                                "quickSort( %d ) takes %1.3f msec", N,
                               (end-start)/1000000.0f ) );

Lab Problem #3: Speeding Up QuickSort

• You should have gone through Problem #2 and modified QuickSort so that you can measure its execution time.
• Name your file Lab12_3.java, and your class Lab12_3 (you will need to submit it to Moodle).
• Run it on sorted arrays of varying sizes until you find an array size that requires between 1 and 10 seconds of execution time.
• Pick one of the methods we saw in class for allowing Quicksort to avoid worst case conditions, and implement it. Modify your code.
• Verify that you have seriously improved your Quicksort function with this mod.

Moodle Submission

• Submit your program to Moodle. Your program will be run against the solution program on a sorted array. The grade is proportional to how close your execution time comes to the execution time of the solution program.